本文详细研究《大航海时代Online》中应该如何把船只航行速度换算为真实世界中航行速度的问题。

真实世界地图制作

地球是一个球体，要把它的表面无变形地展开摊平在纸平面上，谈何容易！现在的地图制作多用投影的方法，就是用一个半透明的地球仪，在地心的位置放上一个光源，在外面套上平面或者圆锥或者圆柱或者合适形状的纸，在纸上描绘出地球仪里照射过来的影子，再把纸展开。

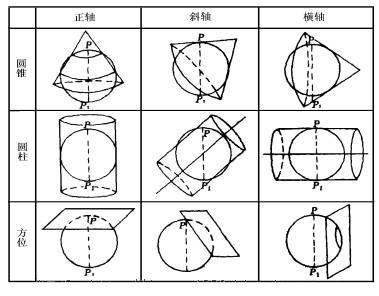
投影的方式有很多种，但是多少个世纪过去了，没有人能找到一种完美的方法，所有的投影都有一定程度的变形。用得比较广泛的是以下几种。

等差分纬线多圆锥投影

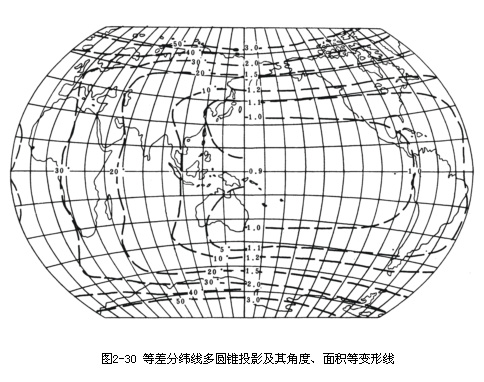
古德投影

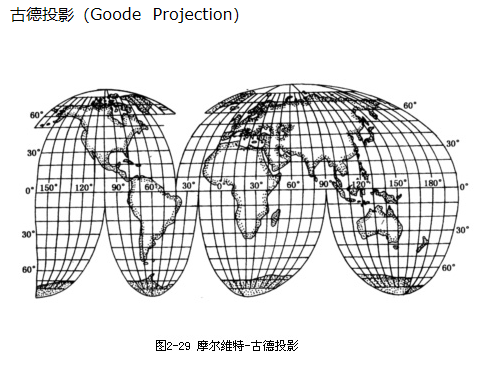
摩尔维特投影

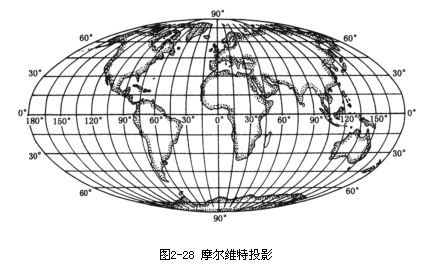
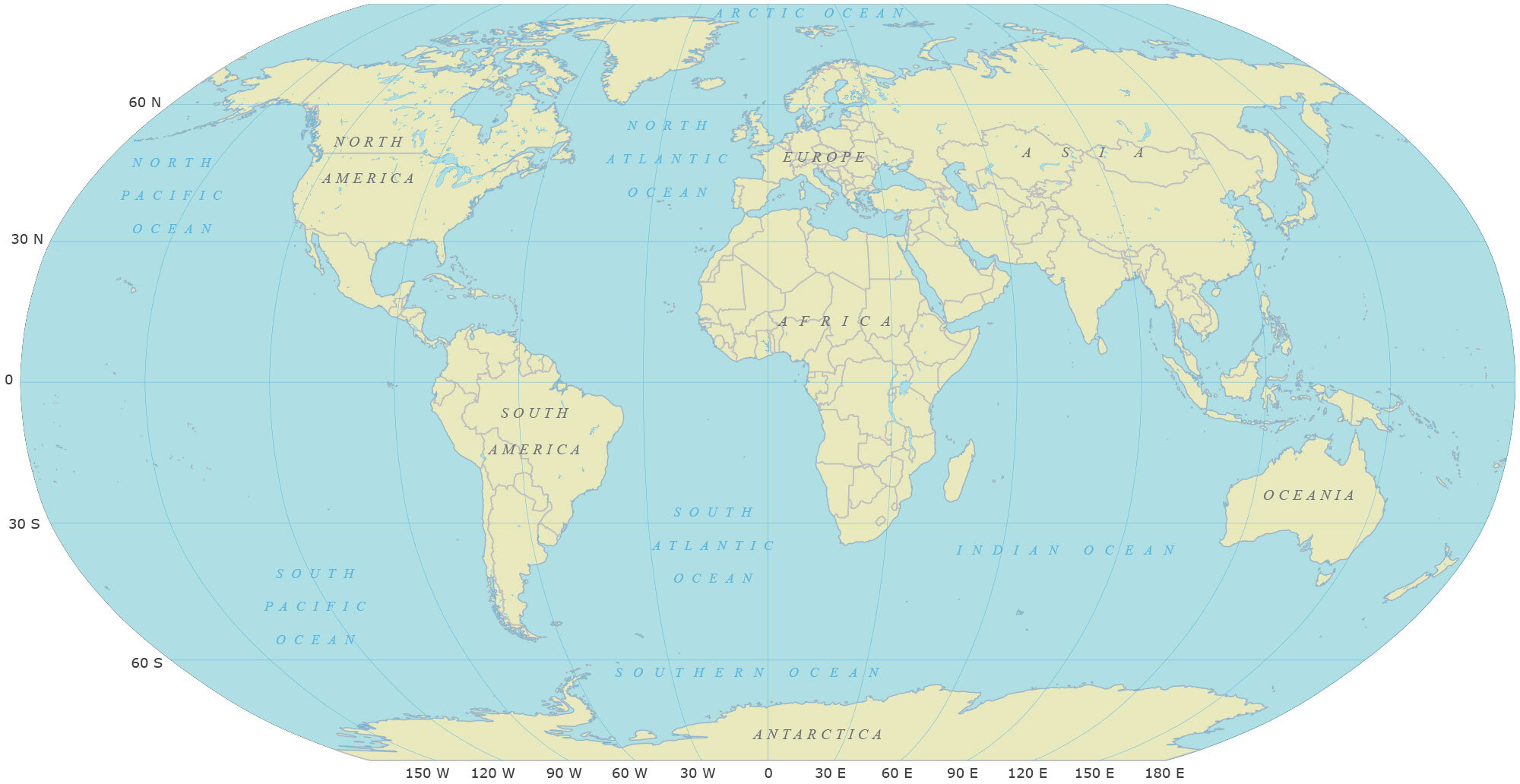
墨卡托投影

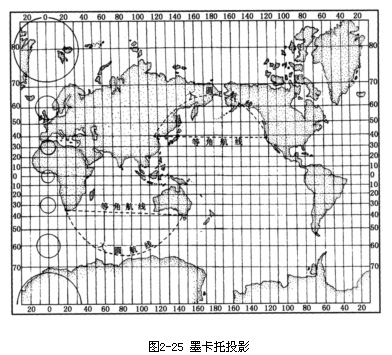
更直白的叫法是圆柱切面投影，这是一种经纬线横平竖直的投影方式，所以它在十六世纪一出现，就立即运用到了航海探险领域。相对来说，这张投影图跟游戏地图最相似，这种长方形的状态也最适合用来做游戏的地图。

让我们来仔细看一下。首先经线之间的距离是相等的，这个很好很强大。但是纬线就差得离谱了，赤道附近小，两极附近大。附带的，地形也跟着变形了，格陵兰岛看上去比南美大陆还要大。这显然跟实际情况不符合，如果要用这张图做游戏地图，就要进行大幅度的修改。高纬度地区要按照一定规则缩小，低纬度地区要按照一定规则放大，当然这都是在保持经纬线横平竖直的前提下做的。

而实际上，地球上的经线之间的距离，在赤道附近最大，越接近两极就越小，到了极点，那当然就是0了。如果我们在保持经线不动的前提下修改了地图的话，两极附近的图形仍然是偏大的。修改的方法是参照等差分纬线多圆锥投影或者古德投影的方式，把经线进行一定程度的弯曲，（局部）朝两极点收拢，最后截去南北极的部分，留下一个长方形就好。

但是这样一来，原先的经纬线就完全被我们破坏了，必须要建立一种新的平面直角坐标系来标记新的地图。游戏中把横坐标0度在伦敦附近，但是不是正好，而是偏东若干距离，这就是前面说的经线被弯曲所导致的结果，我猜想横坐标0度于赤道的交点才是与现实中0度经线和赤道的交点吻合。

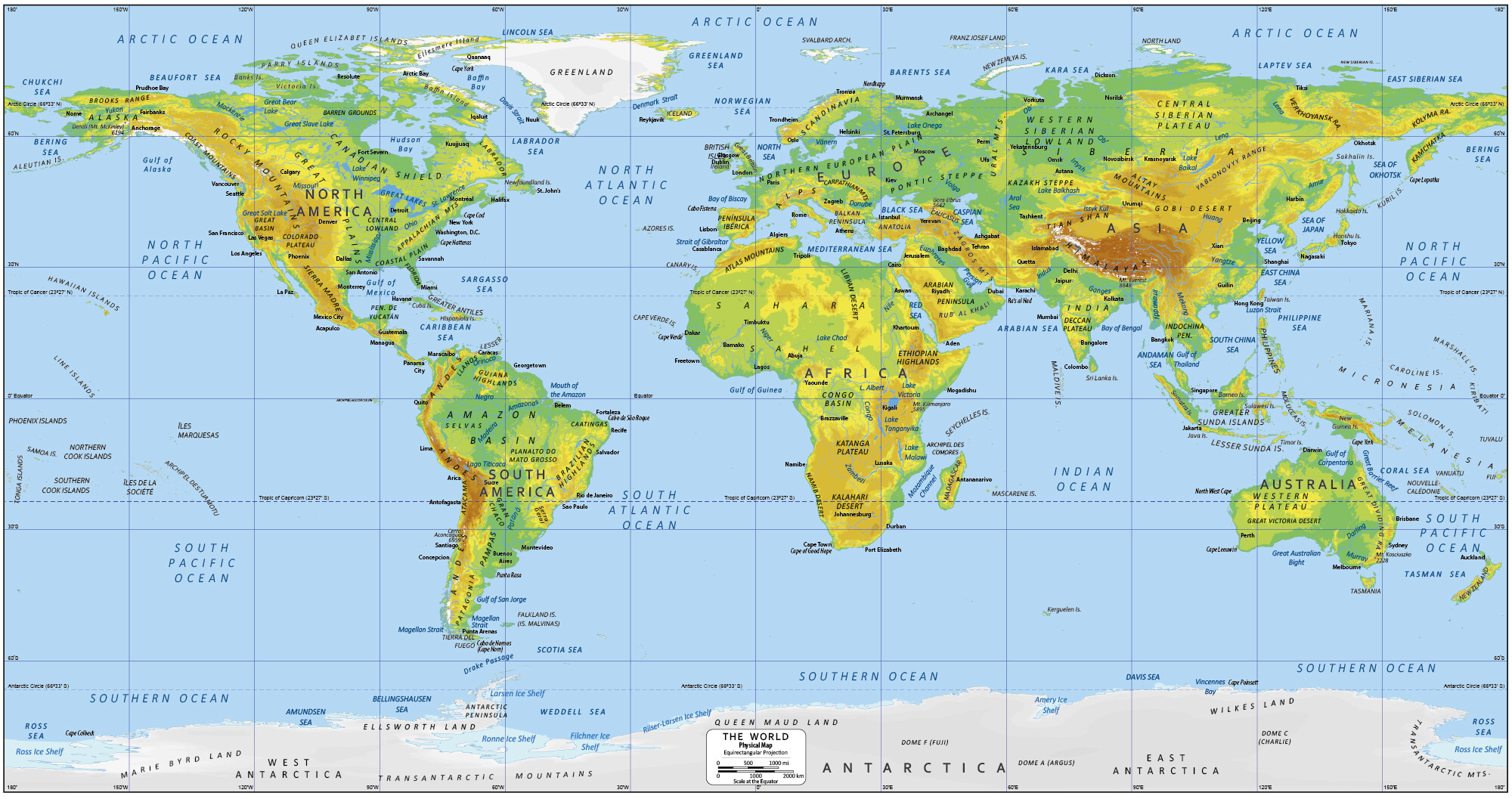
这个新的坐标系有一个很方便的地方，就是它的1经度距离等于1纬度距离，这可以很容易地计算得到两地之间的距离以及航线角。

经纬度

行星的自转使得其呈现“椭球型”：在赤道上凸起，在极点平坦。所以赤道半径比极半径大。

地球的赤道半径a，或长半轴，是从地球中心至赤道的距离，大约为6378.1370km。

地球的极半径b, 或短半轴，是从地球中心至南极或北极的距离，大约为6356.7523km。

在地理学上，椭球体的平均半径计算公式为：

对于地球而言，平均半径为6371.0088km。

经纬线是人类为度量方便而假设出来的辅助线。

纬线

纬线定义为地球表面某点随地球自转所形成的轨迹。任何一根纬线都是圆形而且两两平行。纬线的长度是赤道的周长乘以纬线的纬度的余弦，所以赤道最长，离赤道越远的纬线，周长越短，到了两极就缩为0。纬度表示南北方向的位置。

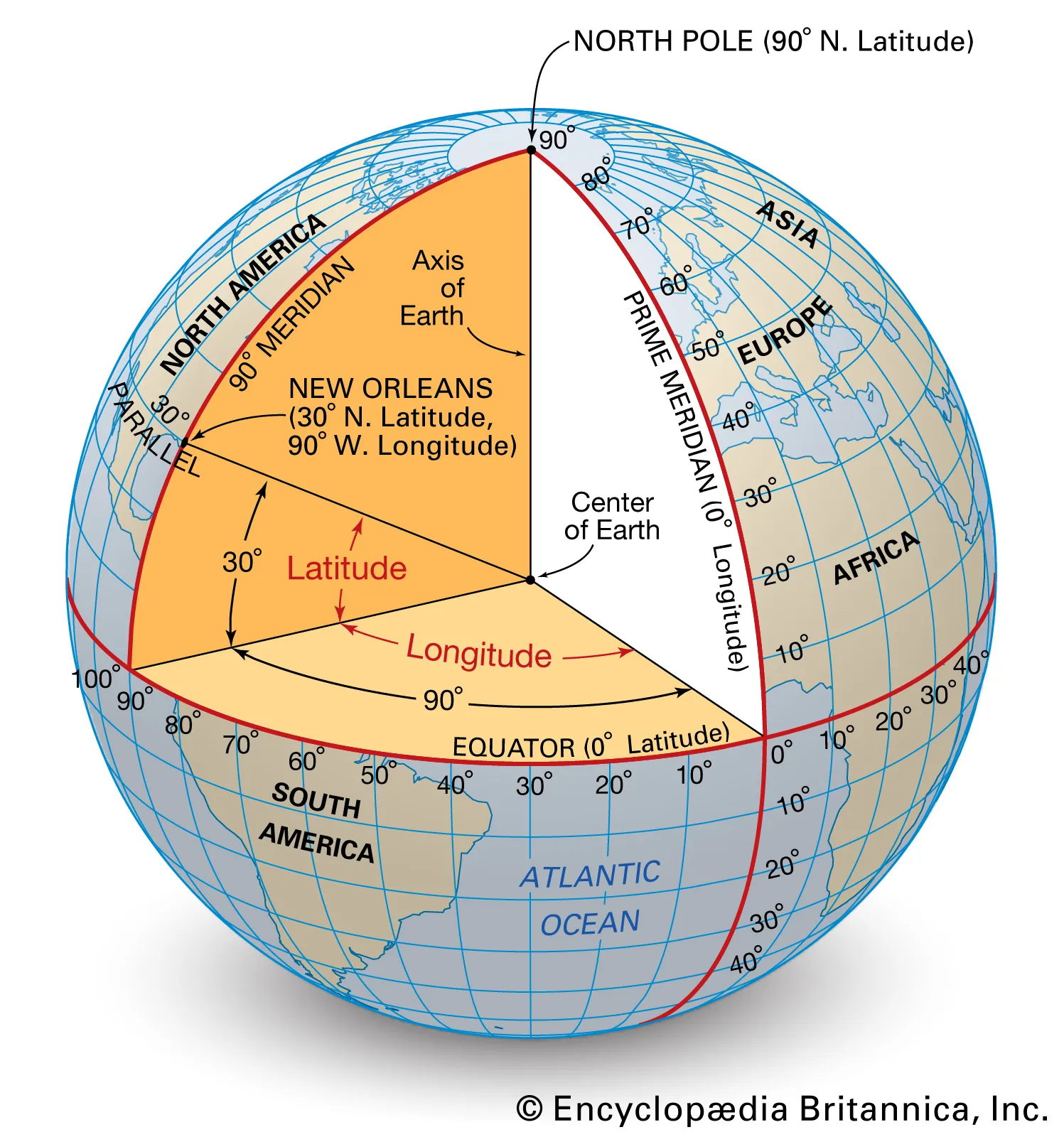
纬度是指某点与地球球心的连线和地球赤道面所成的线面角，其数值在0至90度之间。位于赤道以北的点的纬度叫北纬，记为N，位于赤道以南的点的纬度称南纬，记为S。

任何一根纬线都是圆形而且两两平行。纬线的长度是赤道的周长乘以纬线的纬度的余弦，所以赤道最长，离赤道越远的纬线，周长越短，到了两极就缩为0。

经线

经线也称子午线，定义为地球表面连接南北两极的大圆线上的半圆弧。任两根经线的长度相等，相交于南北两极点。每一根经线都有其相对应的数值，称为经度。经度表示东西方向的位置。

经度是地球上一个地点离一根被称为本初子午线的南北方向走线以东或以西的度数。本初子午线的经度是0°，地球上其它地点的经度是向东到180°或向西到180°。不像纬度有赤道作为自然的起点，经度没有自然的起点而使用经过伦敦格林尼治天文台旧址的子午线作为起点。东经180°即西经180°，约等同于国际日期变更线，国际日期变更线的两边，日期相差一日。

任两根经线的长度相等，相交于南北两极点。每一根经线都有其相对应的数值，称为经度。经线的长度大约为20003.93km。

经纬度

经纬度以度数表示，一般可直接以小数点表示，但亦可把度数的小数点分为角分（1角分等于六十分之一度）和角秒（一角秒等于六十分之一角分），也就是60进制。

1. 度分秒表示（度:分:秒）－49°30’00”-123d30m00s
2. 度分表示（度:分）－49°30.0′-123d30.0m
3. 度数表示－49.5000°-123.5000d（一般会有四位小数）。

经度范围-180～180度，纬度范围-90～90度。

用纬线分割经线，可获知经线单位和公里数的换算表格：

纬度度量	相差距离
1度	111.13km
1分	1.85km
1秒	30.87m
0.1度（6分）	11.11km
0.01度（36秒）	1111.33m

计算任意两个经纬度点的距离

地理空间距离计算方法较多，目前可以分为：

1. 椭球模型，该模型最贴近真实地球，精度也最高，但计算较为复杂。
2. 球面模型，这种模型将地球看成一个标准球体，球面上两点之间的距离即为弧长，这种方法使用较广。
3. 简化模型，这种模型适用于两点距离较近的情形，可以认为两点在一个二维平面上，并且经纬线相互垂直。

《大航海时代online》应该选择简化模型作为计算方法。

球面模型

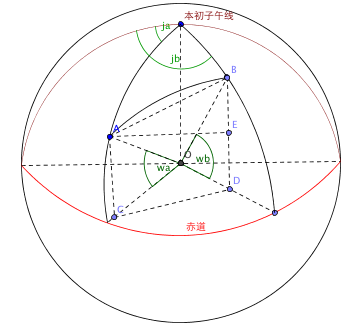
假设地球上有A(ja,wa)，B(jb,wb)两点（ja和jb分别是A和B的经度，wa和wb分别是A和B的纬度），A和B两点的球面距离就是AB的弧长，也叫做大圆距离，AB弧长=R*角AOB（角AOB是A跟B的弧度，O是地球的球心，R是地球半径）。如何求出角AOB呢？可以先求三角形AOB的最大边AB的长度，再根据余弦定律可以求夹角。

1）根据经纬度，以及地球半径R，将A、B两点的经纬度坐标转换成球面坐标

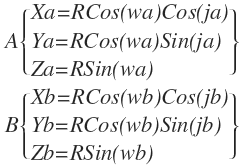
2）根据A、B两点的三维坐标求AB长度

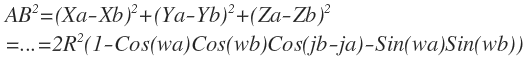
3）根据余弦定理求出角AOB

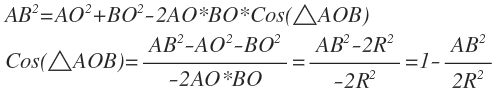
4）于是得到AB弧长=R*角AOB

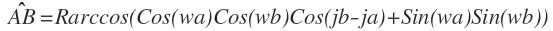
此公式也可以直接使用三面角的余弦定理（Spherical law of cosines）得到，在下文求解两点间的方位角时，我们也会用到这个余弦定理。

这个公式被称为大圆距离公式，但是这个计算公式有有个比较大的问题 ── 当两点相距较近时，cos(jb-ja)的误差会比较大。那么如何解决这个问题？

Haversine 公式

首先，我们先介绍一个三角函数 versine.

Sine, cosine, and versine of angle θ in terms of a unit circle with radius 1, centered at O.

Versine，中文称之为正矢，在三角函数之中被定义为 ，值域在0～2之间。

根据正弦的半角公式：

正矢可以变换为：

由此，我们可以定义正矢的一半，即半正矢（half versine，记为hav）为：

在上述的大圆距离公式的基础上，我们记：

δ=角AOB，即球心角
∆φ=wb−wa
∆λ=jb−ja

有如下的推导过程：

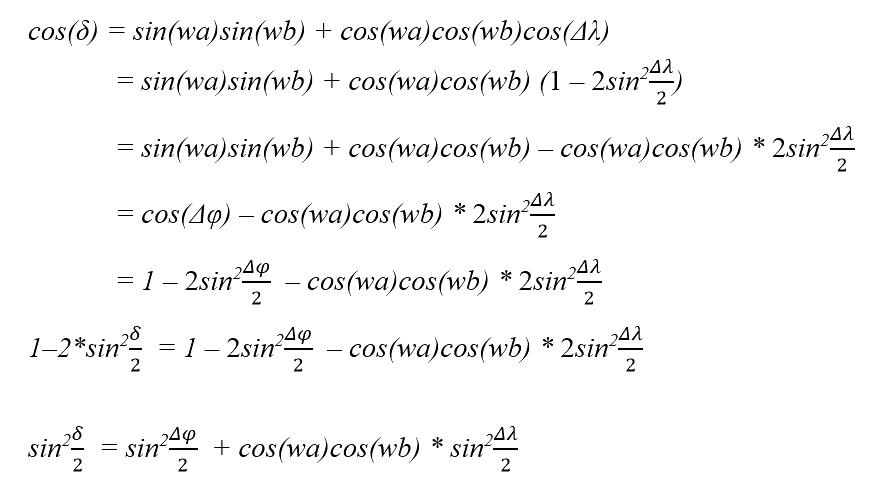
结合上述对半正矢的定义，我们就可以得出如下的Haversine 公式：

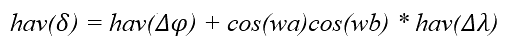
Haversine 公式描述了球面三角形的特性，我们这里不展开叙述。

我们记a为：

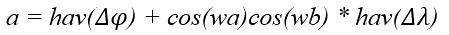
由此，我们可以得到：

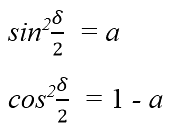
进而得到球心角δ为：

这里atan2是反正切函数arctan的一个变种。

基于值域为的反正切函数，该函数定义如下：

工程上经常使用atan2，目的是确保得到的角度在正确的象限中。

简化模型

简化模型适用于两点距离较近的情形，可以认为两点在一个二维平面上，并且经纬线相互垂直。如图所示，要求A(116.8, 39,78)和B(116.9, 39.68)两点的距离，我们可以先求出南北方向距离AM，然后求出东西方向距离BM，最后求矩形对角线距离。

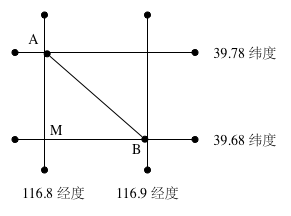
游戏中计算距离和航速

首先要明确现实世界和游戏世界中的航行速度单位。

基本单位

现实中的单位

1海里是地球表面经度上每分维度的距离。

1海里=1.852公里（地球周长40075km，40075/(360*60)=1.85532407407）。

一节航速(Knot)=每小时走1海里的速度=1.852 km/h = 0.5144444 m/s

游戏中的单位

游戏地图满足真实地图制作中墨卡托投影的特点，横纵坐标单位距离相等，横坐标=纵坐标*2。因此可以直接进行单位换算。

测量坐标

使用测量技能时显示的坐标。

横坐标：0～16383共16384个坐标点。
纵坐标：0～8191共8192个坐标点。

1个测量坐标等于360/16384=0.02197265625个经度坐标。
1个测量坐标等于360/16384*60=1.318359375海里。
1个测量坐标等于360/16384*111.13=2.44182128906千米。

内存坐标

游戏程序内部使用的地图坐标。精确度比测量坐标高。换算公式为：

测量坐标 = 内存坐标 * 10000 + 海域偏移值

同一海域内，海域偏移值不变。而计算航速时起点和终点都在同一海域内，因此海域偏移值可以忽略。

1个内存坐标等于360/(16384*10000)=0.000,002,197,265,625个经度坐标
1个内存坐标等于360/(16384*10000)=0.000,131,835,937,5海里。
1个内存坐标等于360/(16384*10000)*111.13=0.000,244,182,128,906,25千米

计算距离

游戏中1天等于现实中1分钟。

根据墨卡托投影及简化模型，只需要使用勾股定理计算两点间距，以及根据两点间的时间间隔，即可计算出航速：

1. 记录两点间的时间间隔和两点坐标。
2. 根据勾股定理计算两点间距，并换算为米。
3. 游戏中时间换算为现实时间，现实时间=游戏时间*60*24。
4. 根据时间间隔计算出多少航速，单位米每秒。
5. 根据需要换算为其他单位航速。
   • 千米每小时=航速3.6
   • 节=航速*0.51

误差

以下原因虽然会产生误差，但都可以忽略不计。

时间计量导致的误差

当计算航速的代码保存瞬时时间时，由于调用函数原因，会导致毫秒级别的误差。

单位换算导致的误差

单位四舍五入会导致误差。

不同单位之间换算会导致误差。

地球形状导致的误差

地球并不是一个正球体，而是一个两极稍扁，赤道略鼓的不规则球体。因此使用墨卡托投影及简化模型会导致误差。

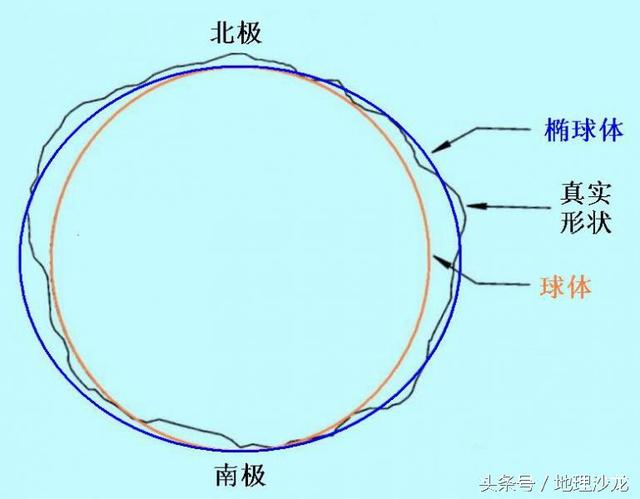
通过实测和分析，终于得到确切的数据：地球的平均赤道半径为6378.38公里，极半径为6356.89公里，测量还发现，北极地区约高出18.9米，南极地区则低下24～30米。看起来，地球形状像一只梨子：它的赤道部分鼓起，是它的“梨身”;北极有点放尖，像个“梨蒂”;南极有点凹进去，像个“梨脐”……被叫做“梨形地球”。确切地说，地球是个三轴椭球体。

https://www.sohu.com/a/148747422_794891

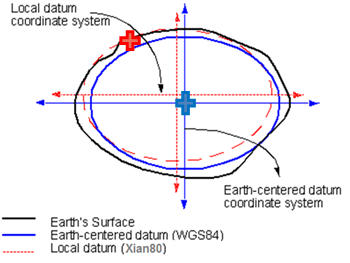
大地基准面是利用特定椭球体对特定地区地球表面的逼近。ArcGIS中，基准面用于定义旋转椭球体相对于地心的位置。大地基准面分为地心基准面、区域基准面。

Ø 地心基准面：由卫星数据得到，使用地球的质心作为原点，使用最广泛的是 WGS 1984。
Ø 区域基准面：特定区域内与地球表面吻合，大地原点是参考椭球与大地水准面相切的点，例如Beijing54、Xian80。

https://blog.csdn.net/weixin_39570530/article/details/111113062

因此，这导致了两个坐标点并不处于大地基准面的同一个平面，造成了高低点垂直方向也就是Z轴的误差。

参考文章

感谢以下作者（不分先后）写作并分享的文章：

• 使用GPS坐标来计算距离和方位角
• 讨论下测量技能得到的坐标数据和真实经纬度的关系
• 地球的奥秘——大航海时代OL里的地理学初探